DPO 直接偏好优化

用监督学习的方式做强化学习的事

🎯 核心概念

来源：强化学习对齐指南：PPO和DPO实施与评估

什么是DPO？

定义

DPO（Direct Preference Optimization） 是一种直接在偏好数据上优化语言模型的方法，无需训练奖励模型，将RLHF简化为类似监督学习的过程。

DPO vs RLHF

特性	RLHF (PPO)	DPO
模型数量	4个（策略+价值+奖励+参考）	2个（策略+参考）
训练复杂度	高（强化学习）	低（监督学习）
稳定性	需要精细调参	相对稳定
计算成本	高	中等
效果	最佳	接近RLHF

---

🔬 DPO原理

来源：RLHF之PPO、DPO详解 | DPO原理深度解析

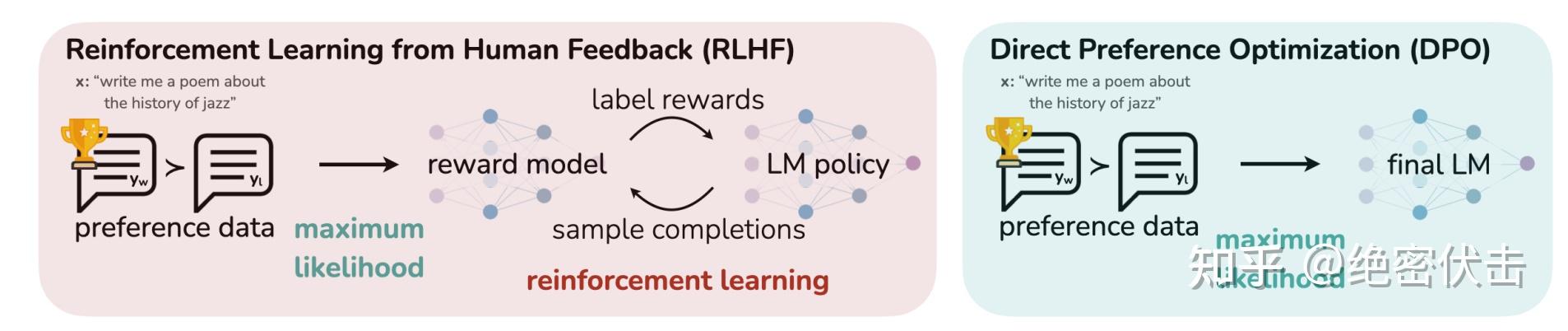PPO 和 DPO 的区别

核心思想

DPO的关键洞察：RLHF 的优化目标存在显式解，可以将奖励函数与最优策略建立解析映射。

从 PPO 到 DPO 的数学推导

Step 1：PPO 的最优策略形式

在 KL 正则化约束下，PPO 的最优策略可以写为：

$$\pi^*(y|x) = \frac{1}{Z(x)} \pi_{ref}(y|x) \exp\left(\frac{1}{\beta} r(x,y)\right)$$

其中 $Z(x) = \sum_y \pi_{ref}(y|x) \exp\left(\frac{1}{\beta} r(x,y)\right)$ 是归一化的分区函数。

Step 2：重参数化奖励函数

将上式对数化并重排，可以得到奖励函数的形式：

$$r(x,y) = \beta \log \frac{\pi^*(y|x)}{\pi_{ref}(y|x)} + \beta \log Z(x)$$

Step 3：代入 Bradley-Terry 偏好模型

偏好数据遵循 Bradley-Terry 模型，代入重参数化后的 $r(x,y)$ 并消去 $Z(x)$，得到：

$$p(y_w \succ y_l | x) = \sigma \left( \beta \log \frac{\pi_\theta(y_w|x)}{\pi_{ref}(y_w|x)} - \beta \log \frac{\pi_\theta(y_l|x)}{\pi_{ref}(y_l|x)} \right)$$

Step 4：最终 DPO 损失函数

$$\mathcal{L}{DPO}(\pi\theta; \pi_{ref}) = -\mathbb{E}{(x, y_w, y_l) \sim D}\left[\log \sigma \left(\beta \log \frac{\pi\theta(y_w|x)}{\pi_{ref}(y_w|x)} - \beta \log \frac{\pi_\theta(y_l|x)}{\pi_{ref}(y_l|x)}\right)\right]$$

其中：

• $y_w$: 偏好的（chosen）响应
• $y_l$: 不偏好的（rejected）响应
• $\beta$: 温度参数
• $\sigma$: sigmoid函数

DPO 本质：将 RLHF 巧妙转化为类似 SFT 的监督学习，隐式学习奖励函数。

直观理解

DPO目标：
  ┌─────────────────────────────────────┐
  │  增加 chosen 响应的概率              │
  │  降低 rejected 响应的概率            │
  │  同时不要偏离参考模型太远             │
  └─────────────────────────────────────┘

---

⚠️ DPO vs PPO 深度分析

来源：DPO vs PPO：深度解读谁是LLM Alignment的未来

虽然 DPO 的推导看似与 PPO 等价，但实际存在几个关键差异：

1. Distribution Shift（分布偏移）

DPO 假设参考分布 $\pi_{ref}$ 能准确捕捉偏好数据分布，但实际中常存在偏移：

问题	DPO	PPO
OOD 数据处理	可能错误提高 OOD 样本概率	KL 正则化抑制偏移
分布假设	依赖 $\pi_{ref}$ 准确性	显式约束偏离程度

PPO 通过显式 KL 正则化限制 $\pi_\theta$ 偏离 $\pi_{ref}$ 的程度：

$$\max_\pi \mathbb{E}{x,y \sim \pi\theta}\left[r(x,y) - \beta D_{KL}(\pi_\theta(y|x) || \pi_{ref}(y|x))\right]$$

2. Reward Hacking 风险

DPO 通过隐式建模奖励函数绕过显式奖励建模，但这可能引入额外的 Reward Hacking 问题：

• DPO 的解集 $\Pi_{DPO}$ 包含 PPO 的解集 $\Pi_{PPO}$：$\Pi_{PPO} \subset \Pi_{DPO}$
• DPO 可能找到符合偏好数据但在实际分布上无意义的解
• PPO 的显式奖励函数和 KL 正则化可减少 Reward Hacking 风险

3. 分区函数缺失

DPO 在推导中省略了分区函数 $Z(x)$ 的显式影响：

PPO：$Z(x)$ 的归一化确保 $\pi^*(y|x)$ 是合法概率分布

DPO：直接消去 $Z(x)$，假设分布足够一致

当参考分布 $\pi_{ref}(y|x)$ 不够准确时，这种省略可能导致对某些选项赋予不合理的高权重。

披萨店类比

• PPO 像严格的朋友：分析每种选择的好坏，结合历史记录，计算综合评分（$Z(x)$ 归一化）
• DPO 像随便的朋友：直接说"A 比 B 好"，但没考虑你对 B 的偏好可能基于伪数据

4. Length Bias（长度偏差）

DPO 可能存在对较短序列的隐性偏好：

$$\log \frac{\pi_\theta(y_w|x)}{\pi_{ref}(y_w|x)} - \log \frac{\pi_\theta(y_l|x)}{\pi_{ref}(y_l|x)} \approx \text{Length}(y_w) - \text{Length}(y_l)$$

解决方案：引入长度正则化项

$$\mathcal{L}{DPO}^{length} = \mathcal{L}(\pi_\theta) + \lambda \mathbb{E}_{(x, y_w, y_l) \sim D}\left[\text{Length}(y_w) - \text{Length}(y_l)\right]$$

结论

维度	DPO	PPO
简化程度	✅ 无需奖励模型	❌ 需要 4 个模型
分布鲁棒性	❌ 依赖 $\pi_{ref}$	✅ KL 正则化
Reward Hacking	❌ 风险较高	✅ 显式约束
长度偏差	❌ 需额外处理	✅ 自然平衡
工业应用	学术实验为主	ChatGPT、Claude 等

结论：DPO 不能完全取代 PPO，至少目前还不能。

---

🔧 DPO实现

使用TRL库

from trl import DPOTrainer, DPOConfig
from transformers import AutoModelForCausalLM, AutoTokenizer
from datasets import load_dataset

# 1. 加载模型
model = AutoModelForCausalLM.from_pretrained("sft_model")
ref_model = AutoModelForCausalLM.from_pretrained("sft_model")
tokenizer = AutoTokenizer.from_pretrained("sft_model")

# 2. 准备偏好数据集
# 格式: {"prompt": "...", "chosen": "好回答", "rejected": "差回答"}
dataset = load_dataset("json", data_files="preference_data.json")

# 3. DPO配置
dpo_config = DPOConfig(
    output_dir="./dpo_output",
    beta=0.1,                          # 温度参数
    per_device_train_batch_size=4,
    gradient_accumulation_steps=4,
    learning_rate=5e-7,                # DPO通常用较低学习率
    num_train_epochs=1,
    warmup_ratio=0.1,
    logging_steps=10,
    save_strategy="epoch",
    bf16=True,
)

# 4. 创建DPO训练器
trainer = DPOTrainer(
    model=model,
    ref_model=ref_model,
    args=dpo_config,
    train_dataset=dataset["train"],
    tokenizer=tokenizer,
)

# 5. 开始训练
trainer.train()

数据格式

{
  "prompt": "请解释什么是人工智能",
  "chosen": "人工智能（AI）是计算机科学的一个分支，致力于创建能够模拟人类智能的系统...",
  "rejected": "AI就是机器人啊"
}

结合LoRA

from peft import LoraConfig, get_peft_model

# LoRA配置
lora_config = LoraConfig(
    r=16,
    lora_alpha=32,
    target_modules=["q_proj", "v_proj", "k_proj", "o_proj"],
    lora_dropout=0.05,
)

# 应用LoRA
model = get_peft_model(model, lora_config)

# DPO训练（使用LoRA）
trainer = DPOTrainer(
    model=model,
    ref_model=None,  # 使用LoRA时可以不需要显式参考模型
    args=dpo_config,
    train_dataset=dataset,
    tokenizer=tokenizer,
    peft_config=lora_config,
)

---

⚙️ 关键超参数

参数	推荐值	说明
beta	0.1 ~ 0.5	温度参数，控制偏离参考模型的程度
learning_rate	1e-7 ~ 5e-6	学习率，比SFT低很多
epochs	1-3	训练轮次
max_length	512-1024	最大序列长度
max_prompt_length	128-256	最大提示长度

Beta参数影响

beta值	效果
小 (0.01-0.1)	更强的偏好学习，可能偏离参考模型较远
中 (0.1-0.3)	平衡（推荐）
大 (0.5-1.0)	更保守，接近参考模型

---

📊 DPO变体

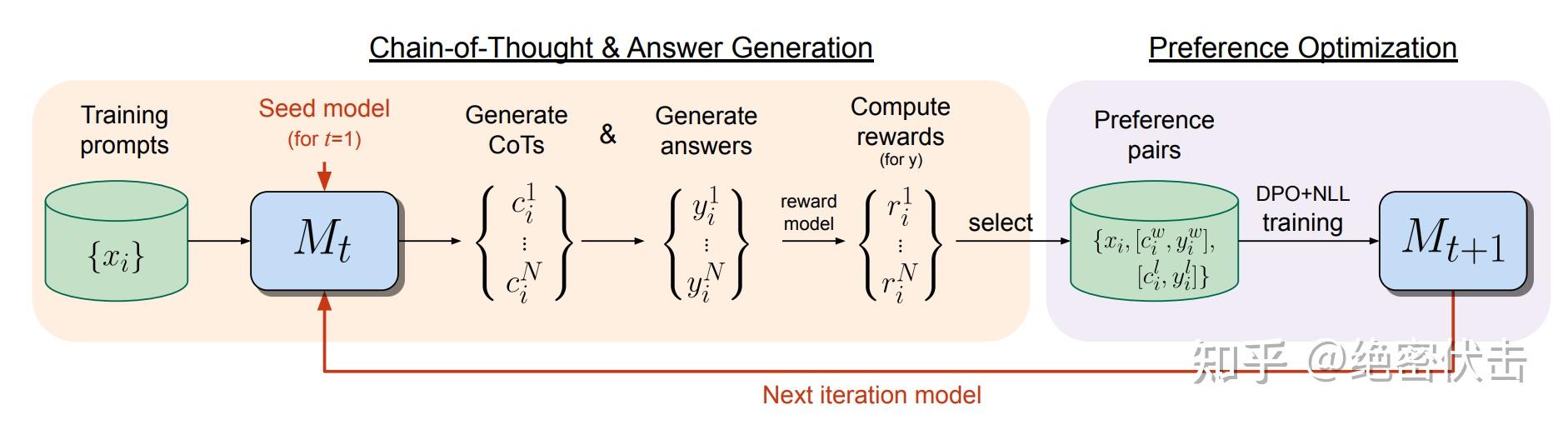Iterative-DPO 流程

Iterative-DPO（迭代式DPO）

2024年 Meta 提出的改进版（Iterative Reasoning Preference Optimization），介于 Online 和 Offline 之间：

1. 训练 Reward Model
2. 将数据分成 m 份
3. 对每份数据：用当前 LLM 采样 k 个回答 → RM 打分 → 选最高/最低构建 pair 对 → 训练一轮 DPO → 更新 LLM
4. 重复直到所有数据训练完成

优势：每轮训练后基于最新模型重新采样，缓解 DPO 的分布偏移问题。

ORPO (Odds Ratio Preference Optimization)

无需参考模型的对齐方法：

from trl import ORPOTrainer, ORPOConfig

orpo_config = ORPOConfig(
    output_dir="./orpo_output",
    beta=0.1,
    # ... 其他参数
)

trainer = ORPOTrainer(
    model=model,
    # 注意：无需ref_model
    args=orpo_config,
    train_dataset=dataset,
    tokenizer=tokenizer,
)

IPO (Identity Preference Optimization)

# IPO使用不同的损失函数
dpo_config = DPOConfig(
    loss_type="ipo",  # 使用IPO损失
    # ...
)

方法对比

方法	需要参考模型	复杂度	效果
DPO	✅ 是	中	很好
ORPO	❌ 否	低	良好
IPO	✅ 是	中	很好
KTO	❌ 否	低	良好

---

🎯 最佳实践

数据质量

def validate_preference_data(sample):
    """验证偏好数据质量"""
    # 1. chosen和rejected不能相同
    if sample["chosen"] == sample["rejected"]:
        return False
    
    # 2. 响应不能过短
    if len(sample["chosen"]) < 50 or len(sample["rejected"]) < 20:
        return False
    
    # 3. 响应需要有实质差异
    from difflib import SequenceMatcher
    similarity = SequenceMatcher(None, sample["chosen"], sample["rejected"]).ratio()
    if similarity > 0.9:
        return False
    
    return True

训练监控

# 关注的关键指标
# 1. rewards/chosen - chosen响应的隐式奖励
# 2. rewards/rejected - rejected响应的隐式奖励
# 3. rewards/margins - 两者差距（应该增加）
# 4. logps/chosen - chosen的对数概率
# 5. logps/rejected - rejected的对数概率

---

🔗 相关阅读

• 训练微调概述 - 了解完整训练流程
• RLHF对齐 - 传统强化学习对齐
• SFT监督微调 - DPO的前置步骤

相关文章：

• 强化学习对齐指南：PPO和DPO实施与评估
• 语言模型对齐技术论述：从PPO到DPO

外部资源：

• DPO原始论文
• Hugging Face TRL DPO
• ORPO论文